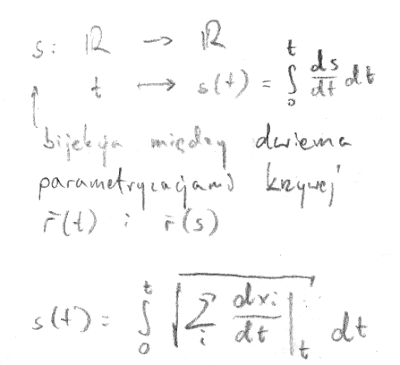arsinh

Każdy chyba czuje, że area sinus hiperboliczy musi mieć coś wspólnego z logarytmem, bo sinus hiperboliczny to z grubsza eksponens. Ich asymptotyczne zachowania są takie same. Przy dążeniu do +∞
więc
Okazuje się że prawdziwy jest związek:
Co ciekawe, nie trzeba wstawiać modułu pod logarytmem, bo liczba pod logarytmem jest wciąż dodatnia (dla x→-∞ ta liczba dąży do 0, czyli logarytm do -∞). Ujemną stronę arsinh odwzorowuje kawałek logarytmu od 0 do 1, i ona jest dokładnie symetryczna do tej dodatniej odwzorowywanej przez logarytm od 1 do ∞. Na pierwszy rzut oka nie widać dlaczego miałoby tak być (ujemna i dodatnia strona logarytmu wyglądają zupełnie inaczej), ale okazuje się ze jest.
Ten wzorek łatwo można pokazać licząc pochodne obu stron:
Pochodne się zgadzają, wartość w np. x = 0 się zgadza.
Kiedyś udało mi się z kolegą z liceum go wyprowadzić licząc na dwa sposoby całkę:Raz wychodzi coś z arsinh, a raz z log. Niestety nie potrafię sobie przypomnieć tego drugiego sposobu. No i jeszcze przydałoby się wyprowadzić analogiczny wzór dla arcosh.

Liczby pierwsze

Co jest szczególnego w liczbach pierwszych?
Najważniejsza własność to to, że każdą liczbę naturalną da się rozłożyć na czynniki pierwsze, tzn. każda liczba jest iloczynem liczb pierwszych. Co więcej, ten rozkład jest jednoznaczny, czyli żaden iloczyn liczb pierwszych nie jest równy innemu iloczynowi liczb pierwszych.
Dzięki temu istnieje bijekcja między a wielozbiorami liczb pierwszych.
Co nam to daje? Na przykład jak chcemy dowiedzieć się czy n jest dzielnikiem liczby m, to rozkładamy obie na czynniki pierwsze i sprawdzamy czy rozkład n zawiera się w rozkładzie m. Jeśli szukamy największego wspólnego dzielnika, to wybieramy po prostu wszystkie powtarzające się liczby (z maksymalnymi krotnościami) z obu rozkładów — czyli przecięcie rozkładów. Jeśli szukamy najmniejszej wspólnej wielokrotności, to po prostu bierzemy sumę rozkładów. W ten sposób skracamy ułamki, wyciągamy liczby przed nawias itp.
Co ciekawe, nie we wszystkich pierścieniach liczby pierwsze mają tą fajną własność. Szczerze mówiąc trudno mi podać jakiś pierścień, inny niż , w którym by miały.

Droga

Żeby odpowiedzieć na pytanie co to jest pochodna wektora wodzącego po drodze, trzeba się zastanowić jak mierzymy długość krzywej.
Weźmy krzywą w R³ w postaci parametrycznej.
Naszą krzywą przybliżamy łamaną.
Następnie każdy wektor odpowiadający odcinkowi przenosimy do przestrzeni stycznej w danym punkcie przez zwykły izomorfizm pomiędzy standartowymi bazami.Ta przestrzeń styczna to zwykły R³, więc możemy w niej liczyć długość naszego kawałka łamanej.
Sumujemy wszystkie uzyskane długości i przechodzimy do granicy. Czyli w skrócie policzyliśmy całkę.
Jeśli s(t) nie ma kawałków stałych, to jest bijekcją, i istnieje funkcja odwrotna s^-1:
W takim razie możemy sparametryzować naszą krzywą parametrem s, i już trywialnie liczyć pochodną po s ze wzoru na pochodną złożenia funkcji:
Jeśli ma się ochotę, konstrukcję s(t) przez łamaną można zapisać trochę inaczej, korzystając z geometrii różniczkowej. Pochodna funkcji w danym punkcie jest odwzorowaniem liniowym przybliżającym ją w tym punkcie.
Czyli w danym punkcie r(t₀) mamy odwzorowanie liniowe R³ → R³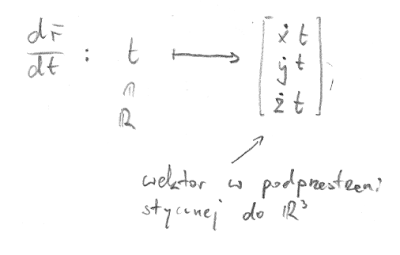
Jest to macierz 1x3. Można myśleć o tym jako o wektorze w przestrzeni stycznej do R³ w punkcie należącym do krzywej — wystarczy podziałać tym odwzorowaniem na liczbę 1, i już mamy odpowiadający wektor.
Możemy zdefiniować w każdym punkcie krzywej wielkość:
Będzie ona miała interpretację prędkości. I już stąd można otrzymać przez całkowanie funkcję o którą nam chodzi:
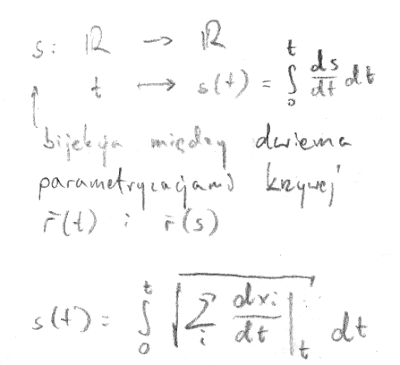
Jest to konstrukcja trochę mniej ogólna, bo nie włożyłem tu możliwości określenia tensora metrycznego zależnego od punktu w przestrzeni, ale generalnie znaczy to samo, tyle że innymi słowami.
Dzięki temu, że mamy zdefiniowane s(t), możemy już powiedzieć co to jest pochodna wektora wodzącego po drodze, czyli coś co fizycy nazywają wektorem stycznym do toru:

Układ współrzędnych

Przedstawię pewne podejście do krzywoliniowych układów współrzędnych. Nie jest to oczywiście pełny obraz, ale pozwala wyrobić sobie pewną intuicję na ten temat, szczególnie jeśli potem dozwolimy na układy odniesienia poruszające się w przestrzeni i obracające.

Prędkość kątowa

Mamy dwa układy współrzędnych, przy czym jeden z nich ma zmienne w czasie wersory. Podstawowa definicja dotyczy różniczkowania w danym układzie współrzędnych (tu primowanym):
Niektórzy oznaczają to d', ale ja wolę notację w kreską. Weźmy wektor, przy czym nie przywiązujemy oznaczeń do wielkości fizycznych, tylko do samych wektorów, a dokładniej do ich współczynników:
Różniczkujemy stronami i z wyniku separujemy pochodną w primowanym układzie.
Dostajemy pewną resztę (dodatek). Tu pojawia się nowe oznaczenie A' — to znaczy po prostu wektor współczynników a_i' (fizycy często oznaczają to po prostu A, bo to jest ten sam wektor, tylko zapisany w innej bazie). Czyli dostaliśmy:
Najciekawsze okazuje się to, że jeśli założymy że każdy z naszych układów jest ortonormalny, to łatwo można ten dodatek zapisać jako iloczyn wektorowy A' z pewnym wektorem (oznaczonym ω) zależnym tylko od pochodnych wersorów e'. Czyli da się opisać tę ewolucję czasową układu primowanego (oczywiście chwilową -- w danym punkcie czasu) niezależnie od współczynników rozkładów wektora A w bazie e i e'. To jest właśnie prędkość kątowa.

Dyfeomorfizmy

Dyfeomorfizm to odwzorowanie klasy C¹, którego odwzorowanie odwrotne też jest klasy C¹. Czasem nazywę pisze się diffeomorfizm (od różniczkowalności). Wiemy że nie zawsze odwzorowanie odwrotne do ciągłego jest ciągłe (np. z odcinka na okrąg), i tak samo jest z różniczkowalnymi. Na przykład x³.
Ma zerową pochodną w zerze, więc odwrotne ma nieskończoną (jest nieróżniczkowalne). F -- lokalny dyfeomorfizm, to znaczy że każdego punku istnieje otwarte otoczenie, na którym F jest dyfeomorfizmem.
Jest bardzo fajne twierdzenie, które działa w wielu wymiarach. Jeśli F' w punkcie x₀ jest bijekcją, to F jest lokalnym dyfeomorfizmem w x₀. Przy czym pochodną w punkcie rozumiemy tu jako odwzorowanie liniowe (macierz):
Bijekcja, czyli detF' ≠ 0. Dla przypadku jednowymiarowego, po prostu ma niezerować się pochodna. Czyli x³ nie jest lokalnym dyfeomorfizmem w x=0, ale jest wszędzie indziej.
Dyfeomorfizmy są izomorfizmami gładkich rozmaitości, i prawdę mówiąc nie znam żadnego lokalnego układu współrzędnych np. na kuli czy walcu, który nie byłby lokalnym dyfeomorfizmem.

Odwzorowania ciągłe

Odwzorowanie ciągłe, to takie które zachowuje granice ciągów, tzn:
Co ważne, odwzorowania ciągłe zachowują zwartość i spójność zbiorów.
Inaczej można ciągłe odwzorowania definiować jako takie, w których przeciwobrazami zbiorów otwartych są zbiory otwarte (przy czym oczywiście chodzi otwartość jako podzbioru dziedziny i obrazu, a nie całych przestrzeni).
Jeśli mamy ciągłą bijekcję, to czy odwzorowanie odwrotne też jest ciągłe? Nie koniecznie. Na przykład odwzorowanie
Jest ciągłe. Ale już odwrotne rozrywa okrąg, tzn. jeśli weźmiemy ciąg zbieżny do punktu (0;0) od strony 2π, to po przekształceniu przez F^-1 dostaniemy ciąg, który co prawda jest ciągiem Cauchyego, ale byłby zbieżny do 2π, a to już jest poza obrazem.
Można to też pokazać tak. Odcinek [0,ε) jest otwarty, traktowany jako podzbiór [0,2π). Natomiast już łuk, który jest odwzorowywany na ten odcinek w okręgu nie jest otwarty -- nie istnieje kula bez brzegu o środku (0;0) całkowicie zawarta w tym łuku. Czyli przeciwobrazem zbioru otwartego nie jest zbiór otwarty.
Można też zobaczyć, że odwzorowanie F zachowuje spójność zbiorów, a F^-1 już nie -- spójne otoczenie punktu (0;0) jest rozrywane na dwa kawałki.

Eksponens sumy

Do tego celu najlepiej zdefiniować eksponens na liczbach zespolonych przez rozwinięcie Taylora:
Jest to szereg potęgowy. Wiemy że szeregi potęgowe są zbieżne w pewnym kole zbieżności. Są tam też bezwzględnie zbieżne (czyli zbieżny jest szereg modułów elementów).
Gdzie lim inf (limes inferior) znaczy granicę infimów ,,ogonów'' ciągu:
Tu to koło ma promień nieskończony. Czyli ten szereg jest zbieżny w każdym punkcie z, czyli jest to dobra definicja. Policzmy iloczyn dwóch eksponensów.Iloczyn dwóch szeregów bezwzględnie zbieżnych można policzyć sumując po prostu wszystkie kombinacje elementów (wystarczy żeby tylko jeden z nich był bezwzględnie zbieżny). Taki iloczyn nazywa się iloczynem Cauchyego. Po prostu dla każdego n bierzemy wszystkie iloczyny w których suma potęg jest równa n, a potem sumujemy to po wszystkich n. W ten sposób przemnożymy każdy element z każdym.
Czyli w zwięzłej postaci
Teraz pozostało nam już tylko przekształcenie tego na dwumian Newtona.Czyli rzeczywiście eksponens sumy to iloczyn eksponensów.

Hipoteza Goldbacha

Hipoteza postawiona w połowie osiemnastego wieku w liście do Eulera. Każdą liczbę parzystą większą niż 2 można przedstawić jako sumę dwóch liczb pierwszych. I tak na przykład:
4 = 2 + 2,
18 = 5 + 13, lub 11 + 7

Co ciekawe, to że do dziś nie udało się stwierdzić czy jest to prawda. W 1900 roku Hilbert przedstawił to jako jeden z problemów milenijnych (razem z hipotezą Riemanna, też mającą związek z liczbami pierwszymi).

Jeśli chcemy przedstawić każdą liczbę naturalną, nie tylko parzyste, to da się to zrobić przy pomocy trzech liczb pierwszych:
6 = 2 + 2 + 2
19 = 11 + 5 + 3, lub 13 + 3 + 3

Da się tak, bo od naszej liczby wystarczy odjąć dwa lub trzy (w zależności od tego czy jest parzysta czy nieparzysta) i otrzymamy liczbę parzystą, która jest sumą już dwóch liczb pierwszych. Oczywiście działa to dopiero od liczby 6.

Ta hipoteza nie ma chyba żadnego praktycznego zastosowania, ale daje nam pojęcie jak dużo można zrobić z liczbami pierwszymi.

Na tym rysunku (z wikipedii) widać na ile sposobów da się rozłożyć daną liczbę parzystą (do tysiąca) jako sumę dwóch liczb pierwszych. Generalnie im większa liczba tym mamy więcej możliwości. Pojawiają się nawet jakieś pasma zagęszczeń.