Eksponens sumy

Do tego celu najlepiej zdefiniować eksponens na liczbach zespolonych przez rozwinięcie Taylora:
Jest to szereg potęgowy. Wiemy że szeregi potęgowe są zbieżne w pewnym kole zbieżności. Są tam też bezwzględnie zbieżne (czyli zbieżny jest szereg modułów elementów).
Gdzie lim inf (limes inferior) znaczy granicę infimów ,,ogonów'' ciągu:
Tu to koło ma promień nieskończony. Czyli ten szereg jest zbieżny w każdym punkcie z, czyli jest to dobra definicja. Policzmy iloczyn dwóch eksponensów.Iloczyn dwóch szeregów bezwzględnie zbieżnych można policzyć sumując po prostu wszystkie kombinacje elementów (wystarczy żeby tylko jeden z nich był bezwzględnie zbieżny). Taki iloczyn nazywa się iloczynem Cauchyego. Po prostu dla każdego n bierzemy wszystkie iloczyny w których suma potęg jest równa n, a potem sumujemy to po wszystkich n. W ten sposób przemnożymy każdy element z każdym.
Czyli w zwięzłej postaci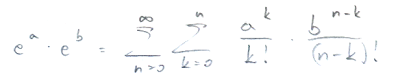
Teraz pozostało nam już tylko przekształcenie tego na dwumian Newtona.Czyli rzeczywiście eksponens sumy to iloczyn eksponensów.

Hipoteza Goldbacha

Hipoteza postawiona w połowie osiemnastego wieku w liście do Eulera. Każdą liczbę parzystą większą niż 2 można przedstawić jako sumę dwóch liczb pierwszych. I tak na przykład:
4 = 2 + 2,
18 = 5 + 13, lub 11 + 7

Co ciekawe, to że do dziś nie udało się stwierdzić czy jest to prawda. W 1900 roku Hilbert przedstawił to jako jeden z problemów milenijnych (razem z hipotezą Riemanna, też mającą związek z liczbami pierwszymi).

Jeśli chcemy przedstawić każdą liczbę naturalną, nie tylko parzyste, to da się to zrobić przy pomocy trzech liczb pierwszych:
6 = 2 + 2 + 2
19 = 11 + 5 + 3, lub 13 + 3 + 3

Da się tak, bo od naszej liczby wystarczy odjąć dwa lub trzy (w zależności od tego czy jest parzysta czy nieparzysta) i otrzymamy liczbę parzystą, która jest sumą już dwóch liczb pierwszych. Oczywiście działa to dopiero od liczby 6.

Ta hipoteza nie ma chyba żadnego praktycznego zastosowania, ale daje nam pojęcie jak dużo można zrobić z liczbami pierwszymi.

Na tym rysunku (z wikipedii) widać na ile sposobów da się rozłożyć daną liczbę parzystą (do tysiąca) jako sumę dwóch liczb pierwszych. Generalnie im większa liczba tym mamy więcej możliwości. Pojawiają się nawet jakieś pasma zagęszczeń.